1494
0
0
2021-09-12 12:26:32
2021-09-12
這周開始了正常的學(xué)習(xí)生活。
這周在科研方面主要看了兩篇論文,，一篇是講量子卷積的,，主要是討論在圖像處理上的量子算法。
而其使用了一種叫QADC的技術(shù),，將振幅信息轉(zhuǎn)換為了經(jīng)典數(shù)據(jù)進行儲存,，如下：
其參考的論文我將作為附件上傳，我感覺是一篇很厲害的文章,。
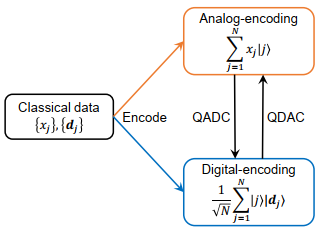
其主要完成了上圖的工作，其中dj是一串01串,，也就是上面Lemma3中的rj
其基本思路是將振幅信息通過swap test轉(zhuǎn)化為了測得輔助量子比特|B? 為0的概率,。而后根據(jù)|B? ，劃分出兩類向量,，在此基礎(chǔ)上構(gòu)建出兩個新的特征向量,。
此時我們就可以對這兩個特征向量的結(jié)果做相位估計,，得到θ的值，而θ的值是與rj 的值有關(guān)的,，這使得我們可以根據(jù)θ推出振幅信息的近似,。
我認為這篇文章工作的最大意義在于其解放了振幅信息的限制，以往要求振幅信息往往需要將其轉(zhuǎn)換為特征向量的形式用相位估計算法來完成,，但這篇文章可以對任意振幅信息進行離散化,，抽取出來并儲存。
參考這個算法在前面的圖像量子卷積上的應(yīng)用,，實際上這個算法完成了矩陣的多核計算,，雖然我暫時摸不清與傳統(tǒng)多核相比其優(yōu)勢在哪。
另外就是我暫時在數(shù)學(xué)推導(dǎo)上沒摸清
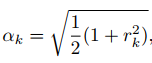
其中αk是測得0的概率,，rk滿足下式
