国产v亚洲v天堂无码久久无码_久久久久综合精品福利啪啪_美女扒开尿口让男人桶_国产福利第一视频在线播放_滨崎步无码AⅤ一区二区三区_三年片免费观看了_大屁股妇女流出白浆_泷川苏菲亚无码AV_我想看我想看一级男同乱伦_国产精品午夜福利免费视频,gogo国模全球大胆高清摄影图,2008门艳照全集视频,欧美午夜在线精品品亚洲AV中文无码乱人伦在线播放

相信LaTeX粉絲對繪圖工具TikZ不會陌生,。在TikZ中,，有一條繪制三次Bézier 曲線的命令

\draw (起點).. controls (控制點1) and (控制點2).. (終點);

卻沒有繪制二次Bézier 曲線的命令,。有人以為,，如果控制點1和控制點2相同,，就得到一個二次Bézier曲線

\draw (起點).. controls (控制點1) and (控制點1).. (終點);

相應地,，該命令可以簡化為

\draw (起點) .. controls (控制點1) .. (終點);

其實,，這種看法是不正確的,。 

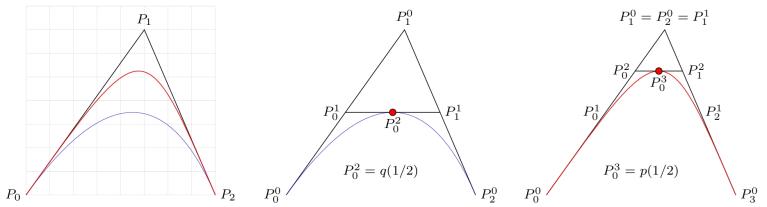
實際上,，以P₀ ,，P₁，P₂ 為控制點的二次Bézier曲線q(t) 和以P₀,，P₁,，P₁，P₂ 為控制點的三次Bézier 曲線p(t)是不同的,?？梢宰C明，只要P₀ ,，P₁,，P₂ 不共線，曲線p(t)就不會退化為二次Bézier 曲線,。

為了能夠在TikZ中正確繪制二次Bézier曲線,，我們可以借助三次Bézier曲線的命令，利用Bézier曲線的升階算法,，定義一個生成二次Bézier曲線的命令 \QuadraticBezier： 

\newcommand{\QuadraticBezier}[3]{(#1) ..controls $(#1)!2/3!(#2)$) and ($(#3)!2/3!(#2)$)..(#3)}

例如,，下圖中的紅藍兩條曲線，就可以分別采用下面兩條語句來實現(xiàn)：

\draw[red] (0,0) .. controls (4,0) .. (2.5,3.5); % 繪制三次Bezier曲線

\draw[blue] \QuadraticBezier{(0,0)}{(4,0)}{(2.5,3.5)}; %繪制二次Bezier曲線

中圖和右圖分別演示用de Casteljau算法計算p(1/2)和q(1/2) 的過程,。